

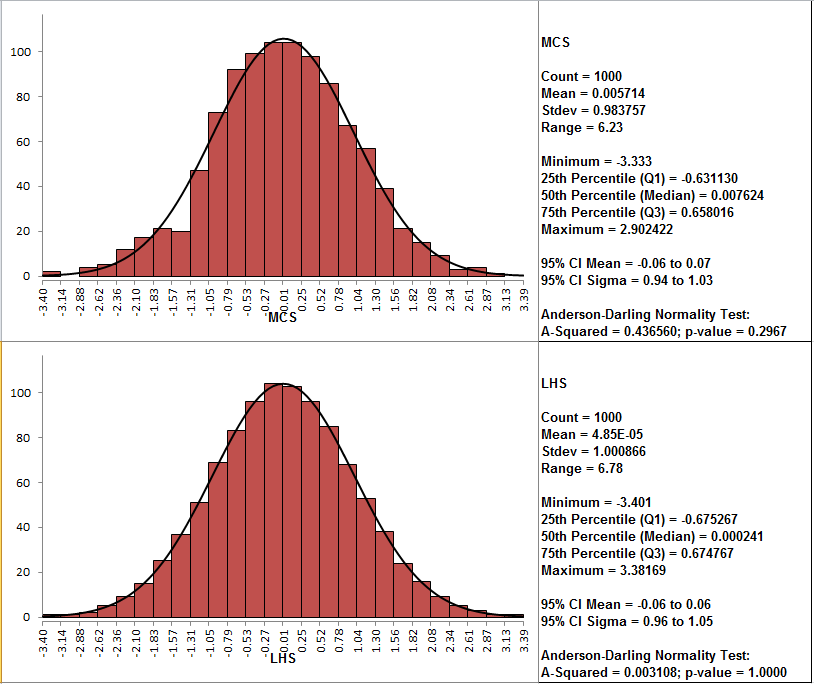
This collection of values forms the Latin Hypercube sample. While a simulation runs, Latin Hypercube selects a random assumption value for each segment according to the segment’s probability distribution. Latin Hypercube sampling divides each assumption’s probability distribution into non-overlapping segments, each having equal probability.

Use Monte Carlo sampling to simulate real world what-if scenarios for your model. Using Monte Carlo sampling to approximate the true shape of the distribution requires more trials than Latin Hypercube. It's the same with the variables that have a known range of values and an uncertain value for any particular time or event (for example, interest rates, staffing needs, stock prices, inventory, phone calls per minute). When you roll a die, you know that a 1, 2, 3, 4, 5, or 6 will come up, but you do not know which for any particular trial. Such random behavior is similar to how Monte Carlo simulation selects variable values at random to simulate a model.
Monte Carlo simulation was named for Monte Carlo, Monaco, whose casinos feature games of chance such as roulette, dice, and slot machines, all of which exhibit random behavior.
Latin hypercube sampling simulation trial#
In other words, the random value selected for one trial has no effect on the next random value generated. The values for each assumption’s probability distribution are random and totally independent. Monte Carlo simulation randomly and repeatedly generates values for uncertain variables to simulate a model.


 0 kommentar(er)
0 kommentar(er)
